モナコインでセルフィッシュマイニングがあったようです。
モナコインへの攻撃から、ブロックチェーンへの攻撃やマイニングを深掘りする
上記サイトが網羅的でわかりやすいので説明はしません。
今回はセルフィッシュマイニングに関して、ハッシュレート、承認数、送金額と不正するインセンティブの関わりを見ていこうと思います。
モデル
内生変数である自身のハッシュレートを\(h\)、外生変数である自分以外のマイナー全体のハッシュレートを\(H\)、ブロックタイムを\(T\)、マイニング報酬を\(R\)、1ブロックマイニングチャレンジするのにかかる電気代を\(W\)とします。
自身がマイニングに成功する確率は
$$ p = \frac{hT}{\left(H+h\right)T} $$
マイニングの期待利得は、
$$ pR – W $$
とできます。
高校数学の重複組み合わせの考え方を使って、
\(z\)ブロックだけhonestチェーンに遅れているattacker チェーンが、途中でhonestチェーンがnブロック伸びるも、追い付く確率は
$$ p_{n,z} = \frac{\left(2n+z\right)!}{n!\left(n+z\right)!} \left(1-p\right)^n p^{n+z} $$
となります。
これらを利用して、
\(n\)ブロックマイニングする期待利得は
$$ n \times \left(pR-W\right) $$
\(n\)ブロックセルフィッシュマイニングする期待利得は、セルフィッシュマイニングしているブロック高で\(x\)だけ送金しているとすると
$$ n \times \left( p_{n,0} \times \left(R+x\right)-W \right) $$
ですから、セルフィッシュマイニングするインセンティブが働く条件は
$$ n \times \left(pR-W\right) < n \times \left( p_{n,0} \times \left(R+x\right)-W \right) $$
これはつまり、
$$ p_{n,0}\times\left(R+x\right)-pR > 0 $$
となります。
サトシナカモト論文
サトシナカモト論文は\(z\)ブロックから追いつく確率をポアソン分布使って示してますが、これだと\(n\)ブロック競り合うことを表現できないので使ってません…。
Octaveで計算する
上記の不等式の左辺を三次元プロットします。
z軸が0より大きいとセルフィッシュマイニングするインセンティブがあるということになります。
octaveのコードはここに置いておきます。
より、\(R=25\)、\(H=1750\)が現実の値ですね。(この記事書いてるとき現在)
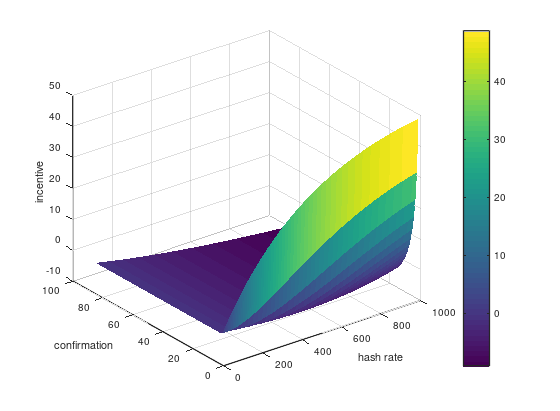
まず、ハッシュレートと承認数に関してみます。
- h=[1,1000] GH/s
- H=1750 GH/s
- R=25 MONA
- x=100 MONA
- n=[1,100] conf
結果が以下です。色はz軸と同じ意味です。
間違いなく、承認数が多いほど不正対策になるということが言えます。
承認数が多いところではハッシュレートが低いほうが高いよりもセルフィッシュマイニングするインセンティブが高いですが、これはおそらく正直にマイニングしてもどうせもうからないからだと思います。しかし、インセンティブが0を下回っているので問題ありません。
承認数が少ないと、ハッシュレートが高いほどインセンティブが増えているのがわかりますね。
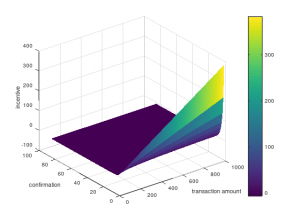
次に、キャンセルさせたい送金額と承認数に関して見ます。
- h=600 GH/s
- H=1750 GH/s
- R=25 MONA
- x=[1,1000] MONA
- n=[1,100] conf
以下が結果です。
送金額が多いほど、不正するインセンティブをなくすには承認数がたくさん必要だということがわかります。
見る限り、200MONAの送金でも20confはほしいところですね。逆にビットバンクのように一括100confはやりすぎかもしれません。(10000MONAくらいの送金で100confくらいが適切になるような気がする。)
まとめ
- 必要承認数が少ないと、ハッシュレートが高いほどセルフィッシュマイニングするインセンティブが高まる
- 必要承認数が少ないと、キャンセルさせたい送金額が多いほどセルフィッシュマイニングするインセンティブが高まる
- 51%なくてもインセンティブは余裕で出てくるっぽい
なので対策としては、少額決済なら少ない承認数で許容、高額決済なら承認数を多くするという直感的にもわかることが正しいと言えます。
また、インセンティブの不等式を\(R\)で偏微分すると負になるので、採掘報酬を上げることによっても不正のインセンティブを下げることができるかもしれませんね。
モデリングでヤバそうなとこあったら教えてください。(結構簡略化もしてます。)
ちなみに、今回の件はPoWかPoSかは関係ないです。関係あるとしたらファイナライズできるPBFTかな。それでもノードの参入制限などトレードオフがあるので適材適所がいいんですよ結局