NEMモザイクの送金手数料は、
・総供給量が多いほど手数料は安くなる
・総供給量が少ないほど手数料は安くなる
という、二つの相反する成分によって計算されます。
で、供給量1~9,000,000,000と、可分性0~6の値域で、どこでもっとも手数料が安くなるのか気になるので、GNU Octaveで4次元グラフにしてみました。
ごりごりの数値計算です。
何回か似たような記事を公開しましたが、おさらいしておきます。
XEMの送金手数料は、送金量を\(x \times {10}^6\)(単位はμXEM)とすると
$$ XemFee\left(x\right) = min \left( 0.05 ceiling \left( \frac{x}{10000} \right) , 1.25 \right) $$
です。これは今回関係ありません。
肝心のモザイクの送金手数料は、総供給量を\(s\)、可分性を\(d\)、送金量を\(x \times {10}^d \)(単位はブロックチェーン内部に保存される最小単位。XEMに対するμXEMのように、一般の表示における\({10}^{-d}\))とすると、
\(s < 10000\)かつ\(d=0\)のときは
\[
MosaicFee\left(x\right)=0.05
\]
それ以外の時は
\[
MosaicFee\left(x\right) = max \left( 0.05, XemFee( \frac{8999999999}{s} \times x) – 0.05 floor \left( 0.8 \times log \frac{9000000000 \times {10}^6}{s \times {10}^d} \right) \right)
\]
です。可分性ってなに?という方は、LCNEMの仕事ついでに、NEMモザイクの仕組みを解剖するをご覧ください。
Octaveのコードの一部を以下に載せます。
function ret = XemFee(x)
ret = min(0.05 * ceil(x / 10000), 1.25);
endfunction
function ret = MosaicFee(s, d, x)
xemEquivalent = (8999999999 ./ s) .* x;
adjustment = floor( 0.8 * log( (9000000000 * (10 ^ 6)) ./ (s .* (10 .^ d)) ) );
ret = max(0.05, XemFee(xemEquivalent) - (0.05 * adjustment));
endfunction
手数料を、供給量、可分性、送金量の3変数関数にしています。
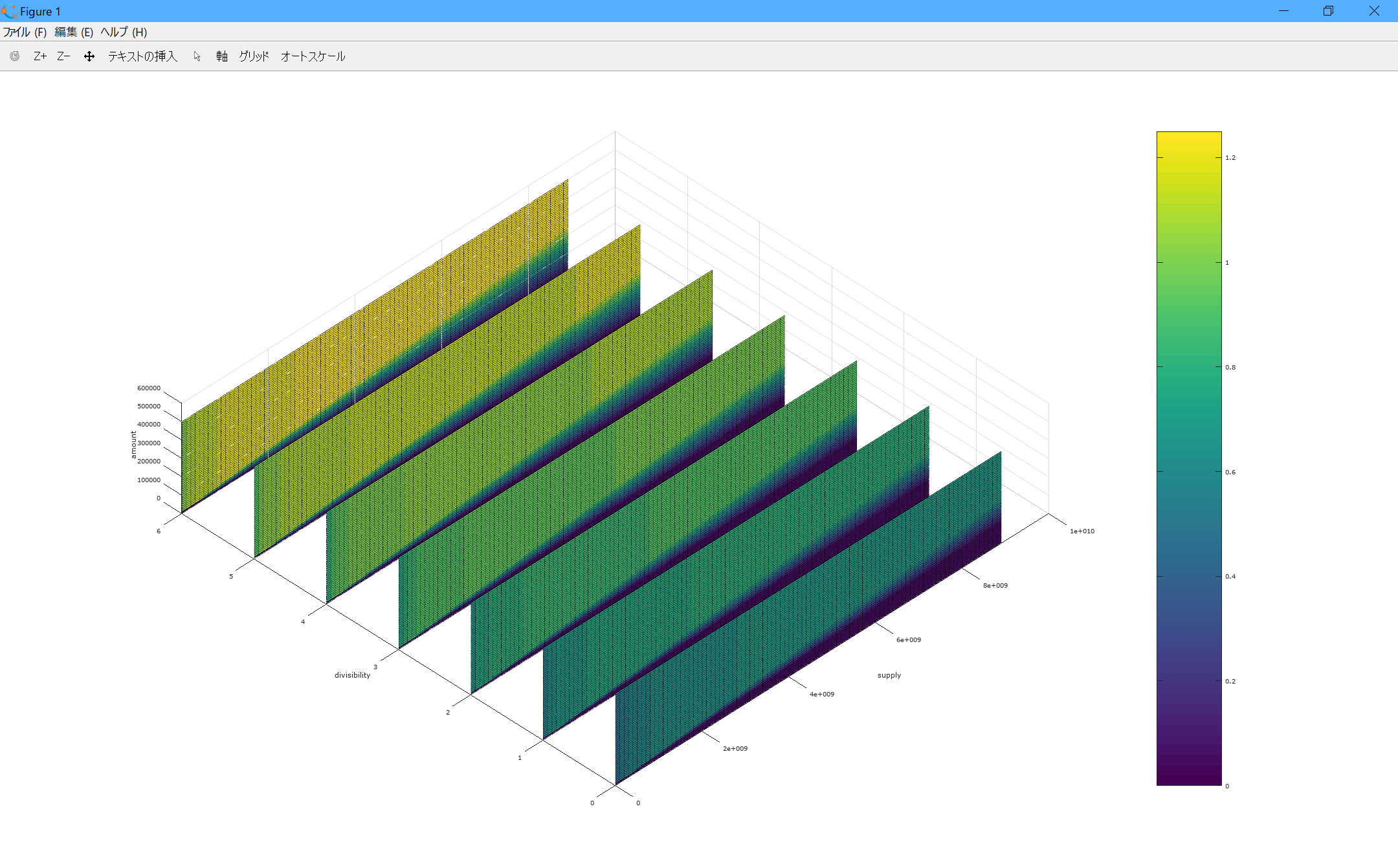
以下、プロット結果です。
色が黄色に近いほど手数料が高いです。スモールビジネスモザイクは考慮していません。
結果として、供給量が多いほど手数料が安く、可分性が小さいほど手数料が安いですね。
モザイクを作る方は、供給量は多めにしておいたほうが良いかもしれないです。