お久しぶりです。
本日、MTPLの論文(ワーキングペーパーなので更新なんでもあり)をDSGEモデル化したアップデート版をSSRNに公開しました。
DSGEモデル化してインパルス応答をシミュレーションするにあたって、OctaveとDynareというソフトウェアを利用しました。
これらの使い方を書き置きしておきます。
まずは、用語説明から。
DSGE
Dynamic Stochastic General Equilibriumの略で、動学的確率的一般均衡モデルとも言います。
主流な経済学の土台となる研究手法となっています。
合理的期待均衡解とか難しいことは省きますが、後述するOctaveとDynareをつかって、経済をシミュレーションするみたいなこともできます。
Octave
Octaveは、リンクを見ていただくのが一番はやいかと思いますが、いわゆる数値計算ソフトウェアです。MATLABと互換性がありますが、MATLABは有料で、Octaveは無料です。
Octave使わない手はありません。
Dynare
Dynareは、経済モデルをシミュレーションするソフトウェアで、OctaveやMATLABのプラグインとして利用します。
インストール
まずはOctaveをインストールしたいところですが、DynareがサポートするOctaveのバージョンは記事執筆時点で4.4.1でした。Octaveの最新バージョンが使えるというわけではないので、DynareがサポートするバージョンのOctaveをインストールするようにします。
次にDynareをインストールします。
Stable versionで構いません。
インストーラに従えば、難なく終わります。
コードの書き方
Dynareのシミュレーションのプログラムコードは.modという拡張子のファイルにテキストエディタで書き込みます。
var
varブロックでは、内生変数を列挙します。内生変数の数と方程式の数は、一致しなければいけません(そうじゃないと方程式解けないですよね)。
varexo
varexoブロックでは、ショックを与えるのに利用する外生変数を列挙します。ショックは後に説明するstoch_simul文で指定します。
parameters
parametersブロックでは、定数となるパラメータを列挙します。
後述するmodelブロックに登場するパラメータのみ列挙すればよいので、途中計算に用いるだけの変数は列挙する必要はありません。
model(linear)
modelブロックには、経済モデルの方程式を書いていきます。
(linear)を指定しない場合、非線形モデルとして扱われ、Dynareが自動で対数線形化を行います。ただし、死ぬほど時間かかるようになり、コンピュータへの負荷もすごいので、手作業で対数線形化して、modelブロックには対数線形モデルを書き、(linear)指定することをオススメします。
癖があるポイントとして、期をまたいだ方程式([latex]t+1[/latex]期と[latex]t[/latex]期の変数が混ざっている方程式)においては、制御理論用語で言うところの状態変数は、未来を時間基準点としてプログラムを書いてやる必要があります。 [latex]t+1[/latex]期の変数にはなにもつけず、 [latex]t[/latex]期の変数には(-1)をつける感じ。逆に、制御変数は、方程式どおり、現在を時間基準点として書きます。
対数線形化
変数[latex]Y_t[/latex]があり、[latex]Y_t=Y_{t+1}=Y_*[/latex]となるような定常値[latex]Y_*[/latex]があるとすると、[latex]Y_t[/latex]の [latex]Y_*[/latex]を基準とした乖離率[latex]\hat{Y}_t=\frac{Y_t-Y_*}{Y_*}[/latex]は、自然対数の1次テイラー近似式[latex]\ln{(x+1)}\simeq x[/latex]を利用することで以下のように表現できます。
[latex]\hat{Y_t}=\frac{Y_t-Y_*}{Y_*}\simeq \ln{\frac{Y_t}{Y_*}}[/latex]といっても、実務的には、
[latex]Y_t=A_t K_t^\alpha L_t^{1-\alpha}[/latex]のように項が1つしかないものであれば[latex]\hat{Y}_t=\hat{A}_t + \alpha \hat{K}_t + (1 – \alpha) \hat{L}_t[/latex]のように、そのまま両辺に自然対数をとってそれにハット記号つければ済みます。 [latex]Y_t=C_t+I_t[/latex]のように項が複数あるパターンは若干面倒ですが、[latex]\hat{Y}_t=\frac{C_* \hat{C}_t + I_* \hat{I}_t}{Y_*}[/latex]のように乖離率の加重平均とすれば済みます。stoch_simul
外生ショックを指定して、インパルス応答をグラフ化して表示します。
合理的期待モデルとして解かれます。合理的期待モデルではなく完全予見モデルとして解くsimul文もありますが、こちらはインパルス応答を表示してくれず、matlab構文でグラフ表示を実装してやる必要があります。
注意したいのは、モデルを対数線形化し、model文に(linear)を指定しないと動かない点です。対数線形化していない非線形モデルの場合、完全予見モデルとしてsimul文でシミュレーションするしかありません。
stoch_simul文の右側、セミコロンの手前には、インパルス応答のグラフを表示する変数を指定することができます。
ちなみに、外生ショックに相関が無い変数だった場合は、指定しても表示されません。
RBCモデルでやってみる
RBCモデルは、基本的な最小構成のDSGEモデル(完全予見として解くと正確にはDGEモデル)です。最小構成すぎて批判も多いですが。
rbc.mod
var A Y K L r w C I;
varexo epsA;
parameters alpha delta rho phi eta;
alpha = 0.5;
delta = 0.01;
rho = 0.01;
phi = 0.9;
eta = 1;
parameters Astar rstar wstar Lstar Kstar Ystar Cstar Istar;
Astar = 1;
rstar = rho + delta;
K_L = (rstar / alpha / Astar)^(1 / (alpha - 1));
Y_L = Astar * K_L^alpha;
C_L = Y_L - delta * K_L;
wstar = (1 - alpha) * Astar * K_L^alpha;
Lstar = (wstar / (eta + 1))^(1 / (eta + 1)) * C_L^(-1 / (eta + 1));
Kstar = K_L * Lstar;
Ystar = Y_L * Lstar;
Cstar = C_L * Lstar;
Istar = delta * Kstar;
model(linear);
A = phi * A(-1) + epsA;
Y = A + alpha * K + (1 - alpha) * L;
r = A + (alpha - 1) * K + (1-alpha) * L;
w = A + alpha * K - alpha * L;
Y = (Cstar * C + Istar * I) / Ystar;
K = (1 - delta) * K(-1) + delta * I(-1);
w = C + eta * L;
C(+1) - C = rstar / (rstar - delta + 1) * r(+1);
end;
shocks;
var epsA = 0.01;
end;
stoch_simul A Y K L r w C I;
main.m
addpath C:\dynare\4.5.7\matlab
dynare rbcこのような2つのファイル構成で、Octaveにてmain.mを実行すると、以下のようなシミュレーション結果が出ます。
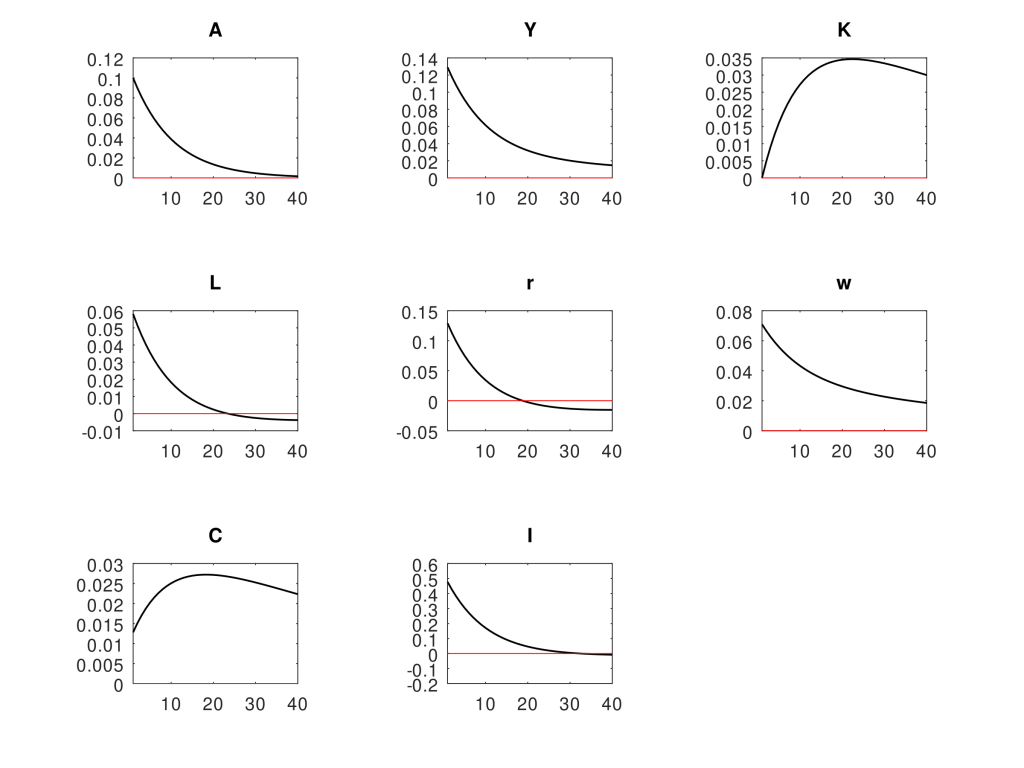
以上です。